Home

Linear Model - Number Lines

Materials: Deck of Fraction Bars per group and one sheet of paper and pencil per person

Place a transparent bar for 2/6 on the overhead and note that the rectangular shape of the bars, as compared to the circular shape of discs or pies, has the advantage that it conveniently extends to a linear model and number lines.

Students often experience difficulty locating fractions on a number line and the Fraction Bars model provides a natural connection to the linear model, as shown in the next group activity.

Group Activity: Drawing Number Lines

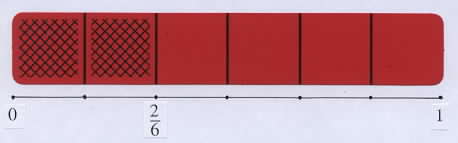
Each person will need a sheet of paper and one of the red bars with 1 to 5 parts shaded for drawing the beginning of a number line. Describe and carry out the following steps at the overhead as each person forms a number line with their bar. 1. Use the edge of the bar to draw a line segment the length of the bar. Mark seven points on the line, one for each of the seven vertical lines of the bar. Label the left end point 0 and the right end point 1, and note that the length from 0 to 1 is called a unit length. 2. Write the fraction for the bar beneath the division line at the end of the shaded amount of the bar. Point out that the end of the shaded amount of the bar indicates where the fraction for the bar should be placed on the line, and this can help students make sense of the placement of fractions.

3. Place the other types of red bars on the line and write the fractions on the line for these bars. 4. Use this unit line segment to measure the length of a small object, such as a pencil, to the nearest 1/6. Discuss rounding to the nearest fraction on the line. If the length of an object is half way between two division lines, such as 4/6 and 5/6, we usually round up to the fraction for the next division. in the following example, the length of the pencil would be rounded up to 5/6.

Discuss this activity and the process of measuring and rounding off to the nearest 1/6. To measure longer lengths, the number line can be extended from 1 to 2 and beyond by repeating the above steps, and by labeling the division points with the mixed numbers 1 1/6, 1 2/6, etc. Discuss the effect of measuring with a number line that is formed using the orange bars: The measurement will be more precise because of the greater number of division points in the unit.

One activity on the Number Lines mats is to move markers along the lines to the end of the mat. The linear nature of the bars is being used on both of the mats below, with one pair of students moving markers according to the shaded amount of a bar, and the other pair marking progress by placing the bars end-to-end.